graphic-深入探索透视投影变换
graphic-深入探索透视投影变换
深入探索透视投影变换
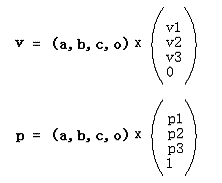
这里*(a,b,c,o)是坐标基矩阵,右边的列向量分别是向量v和点p在基下的坐标。这样,向量和点在同一个基下就有了不同的表达:3D向量的第4个代数分量是0,而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D*几何概念的方式是一种齐次坐标表示。
此外,对于一个普通坐标的点 P=(Px, Py, Pz),有对应的一族齐次坐标 (wPx, wPy, wPz, w),其中w不等于零。比如,P(1, 4, 7) 的齐次坐标有 (1, 4, 7, 1)、(2, 8, 14, 2)、(-0.1, -0.4, -0.7, -0.1)等等。因此,如果把一个点
- 从 普通坐标 变成 齐次坐标,给x,y,z乘上同一个非零数w,然后增加第4个分量w;
- 从 齐次坐标 变成 普通坐标,把前三个坐标同时除以第4个坐标,然后去掉第4个分量。