unity-shader-四元素

分类于 Unity3d-Shader

旋转的表示

那四元数是用来干什么的。四元数是由哈密顿在1843年发现的，但是直到1985年Shoemake才将其引入计算机图形学，四元数的作用极其简单，用来表示3D物体的方位及旋转

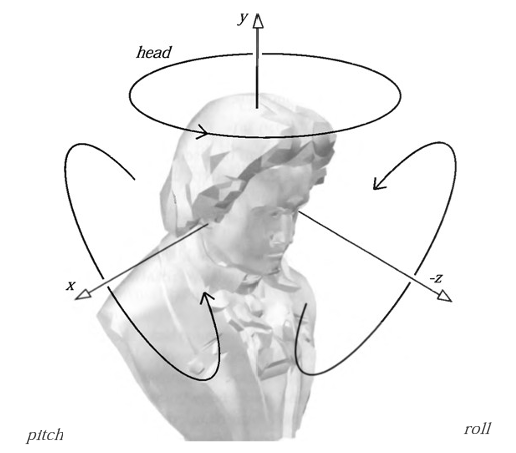
一个3D物体放在世界中，只有一个位置坐标是不够的，这样意味着他总是朝着某一个方向。比如说，我们的头，我们可以摇头，点头，左右卖萌。在三个方向上有3个不同的旋转角度，来确定这个物体的摆向但是这不意味着描述方位和旋转只需要3个量就可以了吗，为什么是四元数而不是三元数？至于这个问题，我不讨论，事实上用3个角度描述方位的办法叫做 “欧拉角”。欧拉角带有各种天生的缺陷，他唯一的优点是比四元数节省（32bit？）。这种形式上的内存节省毫无必要，xnamath的数学库里用的最多的还是xmvector，4个float。但是问题是我们怎么用4个量来描述3个轴上的问题，当然，这时候要请动数学出山理解四元数并不需要真的在3D中去理解，我们可以降维到2D中，2D中是什么，2D中是复数，复数这东西想必大家都学过，也了解各种各样的运算法则，但是你可能错过了复数的一些有意思的地方，容我讲解 (基础的复数知识请自习补充)

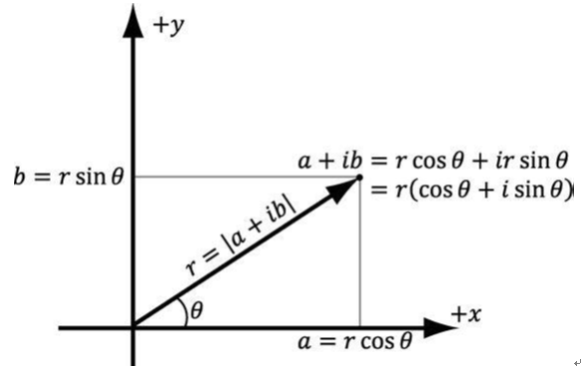
复数在复平面中是一个点,所以我们可以使用极坐标来表示
$$
\begin{array}{c}{r=|a+i b|} \ {a+i b=r \cos \theta+i r \sin \theta=r(\cos \theta+i \sin \theta)}\end{array}
$$
我们现在把两个复数乘起来，但是是以极坐标的方式
$$
\begin{aligned} \mathbf{z}{1}=& r{1}\left(\cos \theta_{1}+i \sin \theta_{1}\right), \mathbf{z}{2}=r{2}\left(\cos \theta_{2}+i \sin \theta_{2}\right) \ \mathbf{z}{1} \mathbf{z}{2} &=r_{1} r_{2}\left(\cos \theta_{1} \cos \theta_{2}-\sin \theta_{1} \sin \theta_{2}+i\left(\cos \theta_{1} \sin \theta_{2}+\sin \theta_{1} \cos \theta_{2}\right)\right) \ &=r_{1} r_{2}\left(\cos \left(\theta_{1}+\theta_{2}\right)+i \sin \left(\theta_{1}+\theta_{2}\right)\right) \end{aligned}
$$
我们使 R2 = 1,
$$
\mathbf{z}{1} \mathbf{z}{2}=r_{1}\left(\cos \left(\theta_{1}+\theta_{2}\right)+i \sin \left(\theta_{1}+\theta_{2}\right)\right)
$$

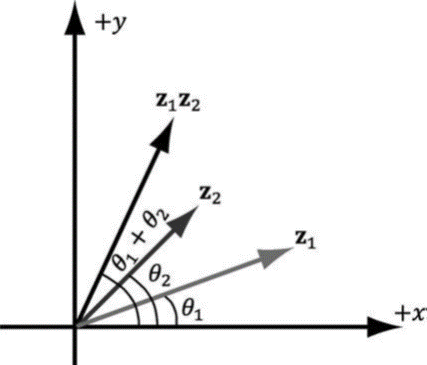
一个复数乘上一个单位复数（模等于1）的结果等于该复数绕单位复数与x轴所成的角度旋转，我们把Z2 作用到了Z1 上面，那么如此同理的结论我们可以推到四元数上面，让我们来看看四元数是在怎么定义的. 四元数和复数差不了太多，唯一的区别是他有三个虚部，他和复数的运算规则大同小异，下图是他的数学定义
$$
\begin{aligned} \hat{\mathbf{q}} &=\left(\mathbf{q}{v}, q{w}\right)=i q_{x}+j q_{y}+k q_{z}+q_{w}=\mathbf{q}{v}+q{w} \ \mathbf{q}{v} &=i q{x}+j q_{y}+k q_{z}=\left(q_{x}, q_{y}, q_{z}\right) \ i^{2} &=j^{2}=k^{2}=-1, j k=-k j=i, k i=-i k=j, i j=-j i=k \end{aligned}
$$